現值/終值/年金是什麼？一次看懂貨幣的時間價值

最後更新：2022-11-07

現值、終值、年金，是進行貨幣時間價值時會使用到的名詞。

由於利率的影響，今天的100元和一年後的100元，兩者價值實際上並不相等，只有透過利率(折現率)將數字調整到同樣時間點之後，才能夠互相比較。

其中現值代表的是現在的價值，終值則是未來最後一期的價值，年金則是每隔相同的時間，收到或付出一筆固定金額的錢。

在金融投資裡面，只要涉及長時間的資產價值評估，例如你要評估一間企業的價值對它做估價，或者評估某項投資的回報好壞，都必須要考慮時間帶來的影響，

其中的計算就會使用到現值、終值、年金、折現率的概念（關於折現率會在下一篇文章做教學）。

這篇文章市場先生介紹現值、終值、年金，分為以下幾個部分：

為什麼要算現值、終值？

首先要知道的是：為什麼我們要知道值、終值？

因為金錢的價值，只有在相同時間點才能互相做比較。

現值考慮到了投資可能獲得的任何利率，因此認為同樣金額的錢，

今天的100元會比未來的100元更值錢，因為投資人可以把今天的100元拿去投資，並預測在未來5年內獲得的報酬率，也就是說今天的100元，會比未來的100元更有價值。

了解到金錢在不同時間價值不同時，如果我們想要做比較，必須把時間點換到同一時間才能比較。

例如，今天的100元和10年後的140元，到底誰好誰壞？
例如，你立刻拿到1500元，跟未來3年陸續拿到450元，到哪個比較好？

你會發現，這些都不能直接比，至少你沒辦法一眼判斷出它的好壞。

但如果你可以把10年後的140元折現到今天算出現值PV，就能和今天的100元做比較。

同理，你也可以把今天的100元折線到未來10年後，算出10年後終值FV，就能和10年後的140元做比較。

這種將未來現金流轉換成現值，或者現金流轉換到未來的過程，就稱為折現(貼現)，

現值是什麼？

現值：未來的所有現金流，價值等於今天多少錢？

現值（英文：Present Value ，簡稱 PV） 是指未來的貨幣在今日的價值，也就是說未來一筆金額，

經過一段時間 折現(Discount)後，算出的現在貨幣價值，白話來說就是未來的1元等於今天多少錢。

其中，折現指的是考慮金錢的時間價值與機會成本，例如有個朋友跟你借100元，那麼他明天就還你100元，與10年後才還你100元，兩者雖然都是100元，但價值並不會相等，

因為如果你今天就立刻拿到100元，可以把它放銀行或投資，會得到利息或投資收益，最終10年後得到的價值會超過100元，

而考慮到時間帶來的差異，所用的調整利率，就稱為折現率。可閱讀：折現率是什麼意思？

現值計算公式？

現值PV = 終值(FV) ÷(1+利率%)^期數 = FV ÷ ( 1 + r )ⁿ

利率通常簡寫為 r  或 i ，期數通常用n期表示，
(在金融領域裡面1期通常是1年，如果不是1年通常會將利率調整為1年)

單筆現值指一筆存款的現在價值，計算方法是將一項投資預期的未來現金流複利折現到現在的價值，
投資人計算時需要知道3個項目：

• 每一期預期的現金流
• 支付現金流的年數(第幾期支付)
• 折現/貼現率(利率)

用來計算現值的利率被稱為折現/貼現率，這是影響現值的重要因素，

折現/貼現率越高、現值越低；折現/貼現率越低、現值越高。

單筆現金流，現值如何計算？

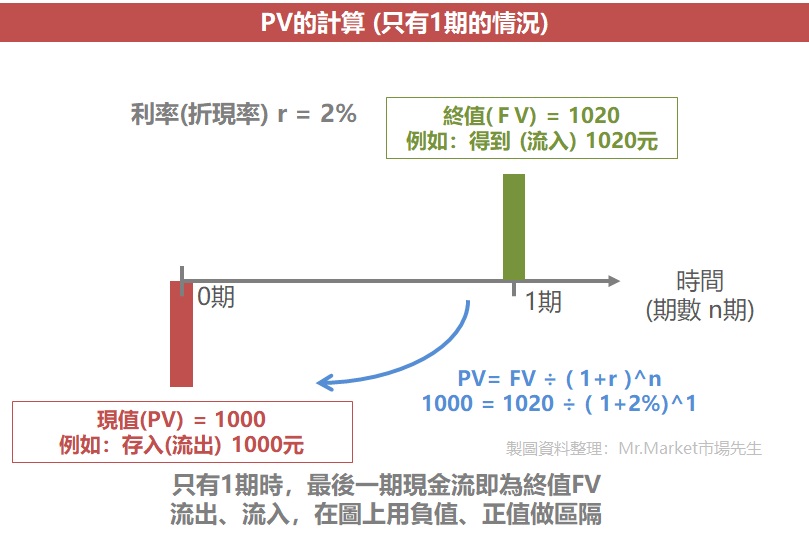
假設你今天以2%的年利率，在一個儲蓄帳戶中投資1,000元，

那麼在一年結束時，它將價值1,020元(1,000元 × 1.02)，包含1000元的本金與20元的利息。

我們可以說：未來一年後 1,020元 ，在2%折現率之下，它的現值是1,000元。

現值可以幫你計算，在每年固定報酬率(%)的計算下，你現在該投資多少錢，才能存到未來的目標金額。

舉例來說：

假設你今天以5%的年利率投資，想在1年後獲得1020元，現在該存多少錢？

計算結果：1,020 ÷(1+5%)^1 = 971.43元，

也就是說需要存971.43元，以5%的利率計算，1年後才能獲得1020元。

多筆現金流，現值如何計算？

上面這是比較簡單的例子，因為未來只有一年，意思是只有一筆現金流 (拿回1000元和利息20元)，因為只有一筆，也可以把它視為終值。

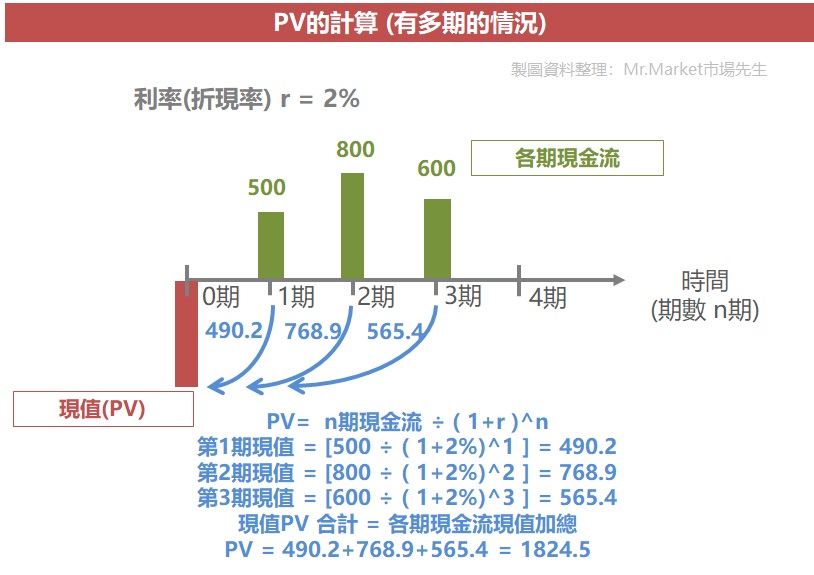
不過一般現值的運算，可能遇到的是未來有數年的現金流，例如說預計第一年收到500元、第二年收到800元、第三年收到1000元，

算法也很簡單，就是把未來每一期的現金流數字分別折現到現在算出現值，再做加總，算出來的就是這些現金流的現值。

現值PV = 各期現金流的現值 加總

各期現金流現值 = 各期現金流 ÷(1+利率%)^期數

下圖舉個例子：

補充：現殖利率因子 PVIF

計算時的期數(n)，通常是一個複利期間，而公式裡的(1+利率%)也被稱為現值利率因子，
表示不同的利率(r或i)與期數(n)所求得到現值利率因子，英文公式會簡寫為 (PVIF r, n)。

現殖利率因子 PVIF = 1 ÷( 1 + r )ⁿ

根據n的不同，這因子會是一個數字。
例如r=5%、n=4時，PVIF=0.823

意思是，你把任意發生在第四期的金額(例如100元)，乘上這個因子的數字(例如100元×0.823=82.3元)，就可以得100元的折現結果是82.3元，

你在書上會看到內容提到現值因子、終值因子等等，算是比較早年的作法，因為西元2000年以前電腦其實還不普及，用計算機來算也很麻煩，把這些因子先算好、數字記錄下來，以後要計算時就方便很多。
現在由於有EXCEL，所以計算很簡單，這類因子大概只剩下學校考試時會用到，通常會提供一張表格，是一種簡化計算的概念。

PV現值與折現率、時間的關係

• 從下圖可以得知，利率越高，現值下降得越快。
• 離到期日(期數n)越遠，現值就越低(逐漸接近於0零)。

折現率越高，時間帶來的貶值就越大、未來的現金流就越不值錢。

例如你錢存銀行，假設利息只有1%，那10年後可能和現在不會多太多，同理10年後的錢折現到今天，也不會貶損太多。
但錢存銀行如果利息有10%，那10年後會差很多，反過來10年後的錢折現到今天，就會貶損很多、沒那麼有價值。

而時間越遠，價值必然越低，如果距今幾百年後才能拿到的一筆金額，即使是一筆巨款，可能它的現值也沒想像中的大。

終值是什麼？

終值(Future Value)：過去的所有現金流，在未來某一期價值多少錢

終值（英文：Future Value ,簡稱 FV）也就是未來價值，它決定了時間對金錢的影響。

簡單來說，終值就是指今天投資的一筆錢，隨著時間的流逝，在一定的利率複利計算下會變成多少錢。

終值的概念，比現值PV來的直覺很多，

例如我們常常談的投資複利，投資數年後最後能拿到的錢，指的就是終值FV。

終值計算公式？

終值(FV) = 現值(PV) ×(1+利率%)^期數 = PV × ( 1 + r )ⁿ

期數 = 經過n期到最後一期
利率通常簡寫為 r  或 i ，期數通常用n期表示。

在算終值時，我們比較不會稱呼利率為折現率，雖然都同樣是利率、意思一樣，

折現率一般只用在計算現值時，對利率的稱呼。

假設你存一筆1,000元在帳戶中，每年支付10%利息，你持有5年的話，未來價值(終值)計算方式為：1,000 ×(1+10%)^5 =1,610.51元

單筆終值計算範例

如果你今天在一個儲蓄帳戶中投資1,000元，年利率為2%，

那麼投資一年後，它的價值變成1,020元，也就是說終值(未來價值)是1,020元。

那麼如果投資2年會發生什麼事？1,000元會變成1044元，

第一年你賺了20元，但第二年卻賺了24元，這額外的4元是第一年年底賺取20元的2%報酬，

而這個賺取利息的過程被稱為複利，它對投資的未來價值有強大影響力。

可閱讀：什麼是複利？

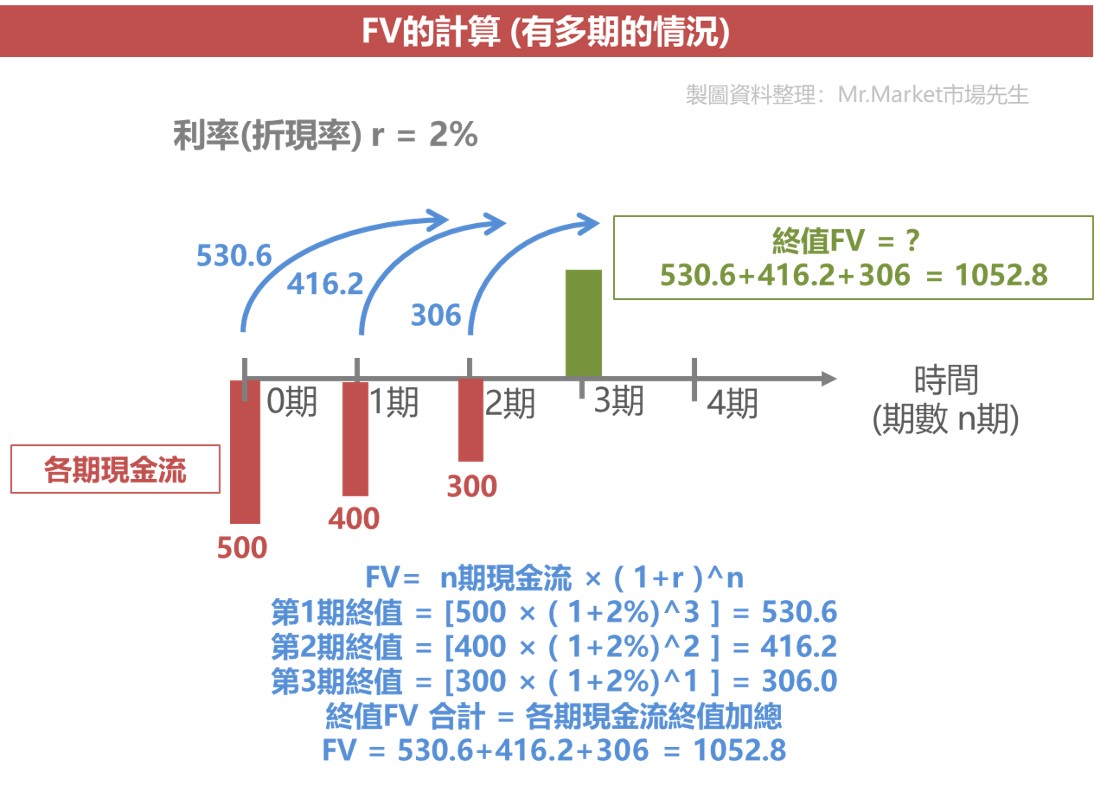
多筆現金流 終值計算範例

舉例，有個投資最初投入500元、第一年投入400元、第二年投入300元，在利率2%的情況，最終一期第三年可以得到多少？

將各期現金流分別計算終值，最後加總，就可以得到合計的終值。

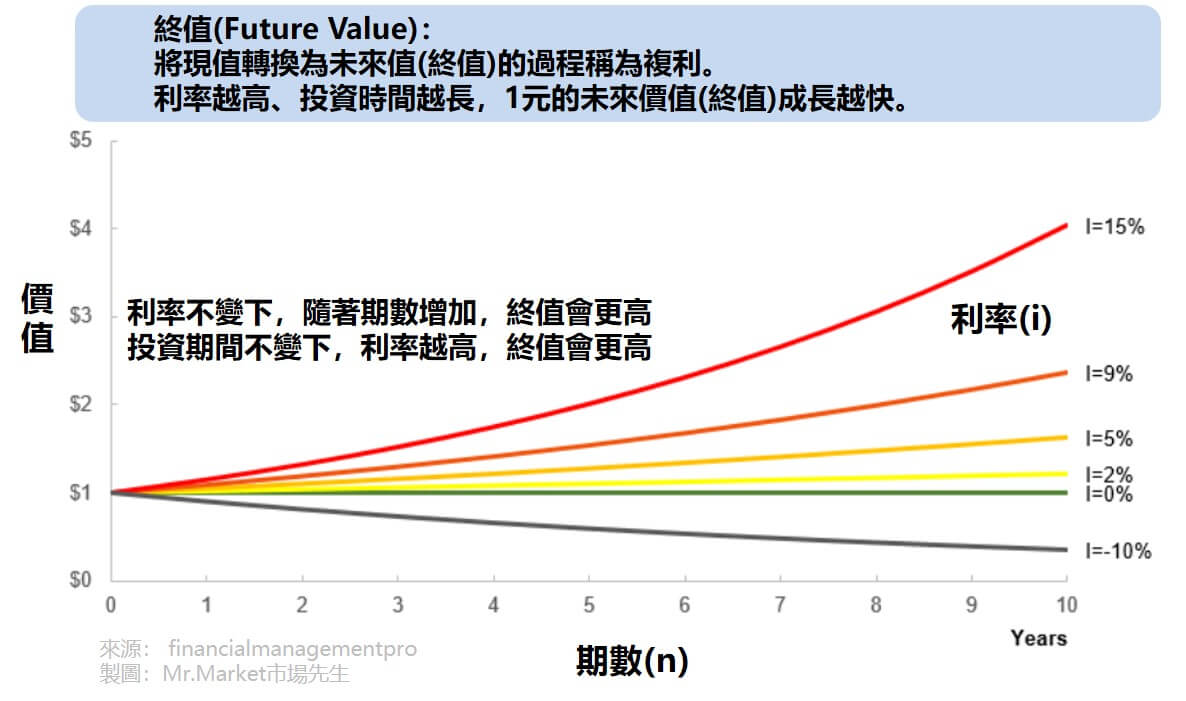
終值與利率(折現率)、期數的關係

從下圖可以看出，當利率越高、投資時間越長，1元的未來價值(終值)成長越快。

年金是什麼意思？

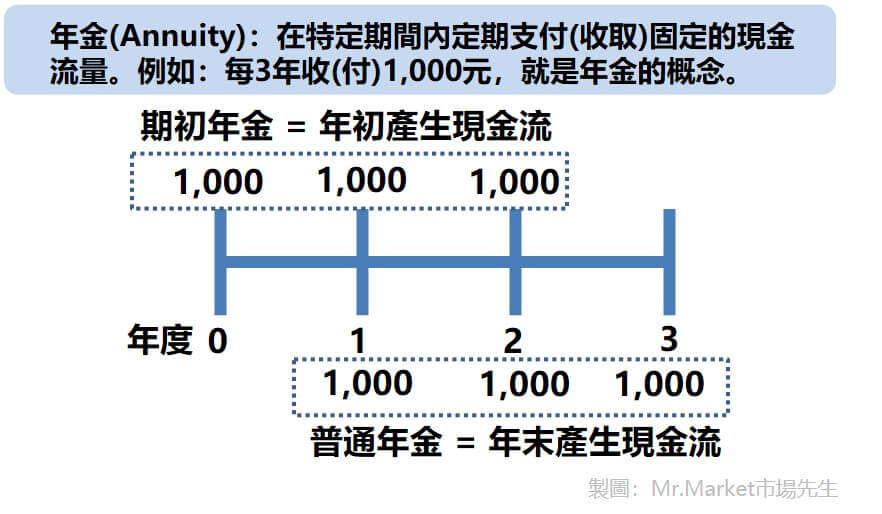
年金(Annuity)：每隔相同的時間，收到或付出一筆固定金額的錢。

年金（英文：Annuity）是指在一定時間內，定期支出、收入的固定現金流量（Payment, PMT），

白話來說是每隔相同的時間，收到或付出一筆固定金額的錢，像是零存整付、房屋貸款、年金給付…等。

一般人最常用到年金的計算，是計算房貸每期要還多少錢，如果每期金額一樣，這就是一種年金。

其次則是把債券、儲蓄險等年金或利息，換算回現值或終值。

年金的定義：

1. 年金每期的收入或支付金額固定不變。
2. 年金的計算期間內，每期現金流量必須持續不能中斷。

年金計算公式的限制很多，因為只要每一期的錢不一樣，年金公式就不能用了，
它只有在現金流一樣時才會用它做計算。

普通年金 vs 期初年金：從第0期開始，還是從第一期開始？

年金又有普通年金、期初年金的分別，

• 若定期支出、收入發生於每期的期末，稱為普通年金；
• 若定期支出、收入發生於期初(第0期)，稱為期初年金。

一般除非有特別說明，否則均指普通年金，

由於這會影響到計算結果，因此計算之前要清楚是哪一種。

1. 普通年金(年末)：年金支出或收入的時間在期末，例如：每月償還的房屋貸款。
2. 期初年金(年初)：年金發生的時間在期初，也稱為即期年金、到期年金，例如：繳交壽險保險費。

期初年金的現金流會比普通年金早一期，

普通年金、期初年金的說明如下圖，普通年金代表支付(收取)的期間在期末；期初年期代表支付(收取)的期間在期初。

「年金現值」與「年金終值」計算

通常我們會在已知年金的情況下，來計算現值、終值：例如已知定期定額的投資(年金)，來計算最後可以得到多少(終值)？

或者在已知現值、終值的情況下，來計算年金：例如借一筆房貸(現值)，計算每期要還多少錢(年金)？

年金現值的意思，是已經知道固定收款金額的未來本利(終值)、利率、計息期數時，

考慮貨幣的時間價值後，計算出這些收付款現在的金額。

年金現值、終值如何計算？

普通年金現值 = PMT × (PVIFA ,r,n)
期初年金現值 = 普通年金現值 × (1 + r)

普通年金終值 = PMT × (FVIFA r,n)
期初年金終值 = 普通年金終值 × (1 + r)

• (PVIFA ,r,n) 年金現值因子= （1 – [1÷(1+r)^n] ）÷ r
• (FVIFA r,n)年金終值因子 = （ [(1+r)^n] -1 ）÷ r
• PMT = 固定現金流 (每一期多少錢)
• r = 利率
• n =期數

要注意，普通年金現值和普通年金終值，都是假定年金發生在每一期的期末，
如果年金是期初(第0期)開始算，就要多乘一期 (1+r)。

其中 PVIFA 、FVIFA稱為年金現值因子、年金終值因子，只要知道利率和期數，就會是一個固定的數字，會寫成例如像是 (PVIFA 5%,6) ，

在學校考試的時候，有時候會給一張表，讓你查這個因子是多少，不過在沒有這種因子表格的時候，就是自己用公式算。

年金計算公式如下圖：

FV其實就是把PV值在乘上 (1+r)ⁿ。

一般來說這公式，除了學校考試以外是不用背的，會用EXCEL算或者需要時再查就好。

但是現值和終值轉換這個就很基本，一定要知道怎麼算。

年金現值計算例子：

假設從年初開始，持續投入1,500元年，利率為5%，總共投入6年，該如何計算最初年初的現值？

先計算普通年金現值 = 1,500 × (PVIFA 5%,6) = 1,500 × 5.0757 =7,613

7,613是每期期末開始投入的期況，因為題目的投入是期初開始，所以計算上要調整，多乘以一次利率，

期初年金現值 = 7,613 × 1.05 = 7,994元

年金終值計算例子：

假設你在年初存了1,500元，總共存6年、年利率為5%，每年計息1次，那麼在第6年年底時終值是多少？

先計算普通年金終值 = 1,500 × (FVIFA 5%,6) = 10,202

同樣的，10202元是假設期末投入的情況，但因為題目是期初投入而非期末投入，所以要多乘一次利率。

期初年金終值 = 10,202 × 1.05% = 10,712元

年金如何計算？

年金PMT = PV ÷ (PVIFA ,r,n)

年金PMT = FV ÷ (FVIFA r,n)

• (PVIFA ,r,n) 年金現值因子= （1 – [1÷(1+r)^n] ）÷ r
• (FVIFA r,n)年金終值因子 = （ [(1+r)^n] -1 ）÷ r
• PMT = 固定現金流 (每一期多少錢)
• r = 利率
• n =期數

市場先生提示：現值、終值、年金 應用與注意事項

下列幾點觀念在終值、年金計算都是通用的。

1. 用現值來評估估價是否合理？

現值最大的用意，是幫投資人判斷一項投資支付的價格是否合適，
如果算出來的未來回收的現值低於付出成本的現值，那麼這個投資就是不合理的。

例如，你對一檔股票做估價，折現率用你的投資機會成本5%去估計，
假設考慮到這企業未來現金流折現後，價值是200元，但現在股價高達300元，這時就代表你投資時，除非最後實際現金流高出你的預期，否則最終你如果買在300元，得到的報酬率就會低於5%，也就是不值得投資。

知名的DCF現金流折現估價模型，就是在計算現值PV。

而許多估價方法，如本益比法，其實都是這種折現模型的簡化版本。

可閱讀：現金流折現估價模型DCF是什麼？

2. 折現最重要的問題：折現率該用多少？

在現值的計算公式中，利率%就是現值的折現/貼現率，也就是用來計算現值的投資報酬率，
但計算現值的折現/貼現率其實是非常主觀的，
因為它是預期你把今天的錢投資一段時間後，將會得到的預期報酬率，
換句話說，也就是機會成本。

機會成本有非常多種可能，常見的如下：

• 無風險利率：無風險的報酬率常用來當折現/貼現率，利率代表了投資或專案需要賺取的報酬率。
  假設2年期公債支付2%的利息或報酬率，投資人的投資標的至少需要賺取超過2%的收益才合理。
• 投資的機會成本：你本身資金有其他選擇，例如你有另一些風險類似投資機會，當中最好的至少有5%報酬，5%就是你的機會成本。
• 風險資產定價模型：當承擔不同風險時，會根據無風險利率，加上一定程度的承擔風險要求報酬。簡單舉例如無風險利率2%，再加上根據承擔額外風險的要求報酬4%，2%+4%=6%報酬，作為折現率。如果是波動更大、風險更高的投資，應該要求更高報酬來補償風險，例如額外要求報酬8%，折現率用 2%+8%=10%來算。
• WACC加權資金成本：一般是企業取得資金的成本，例如銀行或者債券借款利率是6%，投資人要求報酬則是8%，那企業想做一個投資、取得資金的成本，就是這6%和8%根據比例加權出一個權重(假設7%)，這7%就是機會成本，可以做為折現率。

可閱讀：折現率是什麼？

3. 要考慮通膨影響

只要是貨幣，就會受到通貨膨脹影響。

在計算時我們算的通常是用名目利率做計算，也就是不考慮通貨膨脹的利率(折現率)。

實際上算出來後，未來100元的金錢購買力也不會等於今天100元的購買力。

如果要考慮到貨幣購買力，計算時要把使用的利率，再扣掉預期通貨膨脹減損，這種利率(折現率)稱為實質利率。
例如你原本預期名目利率(折現率)5%，但如果想考慮到通膨2%，實質利率就要調整成 5% – 2% = 3%。
最終用實質利率算出來的，就會是考慮跟當下貨幣實質購買力一樣可比較的結果。

但一般計算時仍是用名目利率為主，原則上不會用實質利率做計算，
因為如果用實質利率算，這會導致無法與其它的一些沒考慮通膨的數字做比較，且算出來是購買力，也不是真正得到的金額。

4. 一切都是假設與估計

無論是未來的現金流，或者折現率，都是一種估計和猜測，並非絕對精準的計算。

例如，你可以算出一個債券未來利息現金流和償還本金，將年金和終值轉換為現值，如此一來可以做出估價，
問題是你沒有考慮違約、錢付不出來的狀況？

市場先生在這裡再次提醒，不要忘記估計就只是估計。

這也是為什麼投資時除了估價法，還要考慮安全邊際，這就是為了錯誤而預留的空間。

可閱讀：什麼是安全邊際？

現值、終值、年金EXCEL計算工具

在做現值、終值、年金計算時，你至少要知道現值、終值的計算公式，這可以很簡單按計算機計算。

如果是學校考試，通常會給現值因子、終值因子、年金因子的參數表，可以查表計算。
(但市場先生自己學校畢業後，還從來都沒查過表，需要時都是用EXCEL算居多，用因子查表算是古時候常用的方式)

複雜一點涉及多期現金流、年金的情況，通常會用EXCEL做計算比較快。

這裡分享一份EXCEL，有需要的可以自行下載來運用，
裡面也有EXCEL公式，看懂公式和參數候你就可以自己做許多運算。

EXCEL內建有包含現值PV、終值FV、年金PMT、利率Rate、期數nper，
基本上你只要輸入其他已知的變數，就能算出剩下未知的項目。

現值、終值、年金 計算EXCEL
下載：現值、終值、年金 EXCEL計算工具 (雲端硬碟點選右上角有下載按鈕)

EXCEL和我們一般計算最大的差異在於，流出的資金你要輸入負值(比方說每期支付款項)，流入的資金則是正值(比方收回的金額)。

當然，有時候年金會很複雜，各種金流每期價值不等，需要自行計算加總起來，這類型的狀況並沒辦法套用現成的公式，
這時候就只能一期一期算，當然如果你會寫EXCEL公式在計算上就會輕鬆許多，其實也就是加減乘除，不過這個就沒辦法提供範例。

快速重點整理：現值、終值、年金是什麼？

1. 現值是未來的所有現金流，價值等於今天多少錢？
2. 今天的100元會比未來的100元更值錢，這差異來自於利率與時間，利率在計算時也稱為折現率。
3. 終值是過去的所有現金流，在未來某一期等於多少錢？
4. 年金是每隔相同的時間，收到或付出一筆固定金額的錢。
5. 年金計算有普通年金、期初年金的分別，若定期支出、收入發生於每期的期末，稱為普通年金；若定期支出、收入發生於期初，稱為期初年金。
   一般除非有特別說明，否則均指普通年金。計算時要注意年金發生在哪一期。

市場先生心得：整理這篇現值、終值、年金，是因為，最近開始寫到許多涉及金融計算的文章，都會用到這些基礎的計算概念，
先寫好一篇，以後才不用每一篇文章都要花很多力氣解釋。

我自己學到現值、終值、年金、折現等觀念是許多年前在大學的時候，
第一次學習的時候裡面其實「終值」最直覺，而「現值」相對比較不直覺、較抽象，
而年金大多都是計算時使用，真實世界用到年金的情況其實不多，因為許多每年能拿到的現金流，每期的錢可能並不相等，簡化的公式實際運用場景很有限。

但如果你能搞懂現值、終值、年金，相信你對金融市場所謂的金錢時間價值關係，就會有更完整的體會。

下一篇：折現率是什麼？

更多投資入門學習：

1. ETF投資教學懶人包

2. 基金投資教學懶人包

3. 理財第一堂課：認識現金流

4.  我的投資理財書單分享

5. 美股ETF線上課程

加入市場先生FB社團，充實更多理財好知識

50歲之前想退休一定要懂理財，
解決投資的煩惱！

最近市場先生開了一堂的「用美股ETF創造穩定現金流」教學課程，
這堂課程會從基礎入門、資料查詢到實際操作，
教你學會建立一個穩定的全球ETF投資組合，目前累積已經有將近1100位同學上課。

線上課程》美股ETF創造穩定現金流線上課程連結

如果覺得這篇文章有幫助，
幫我按個讚，分享給更多人看到，謝謝！